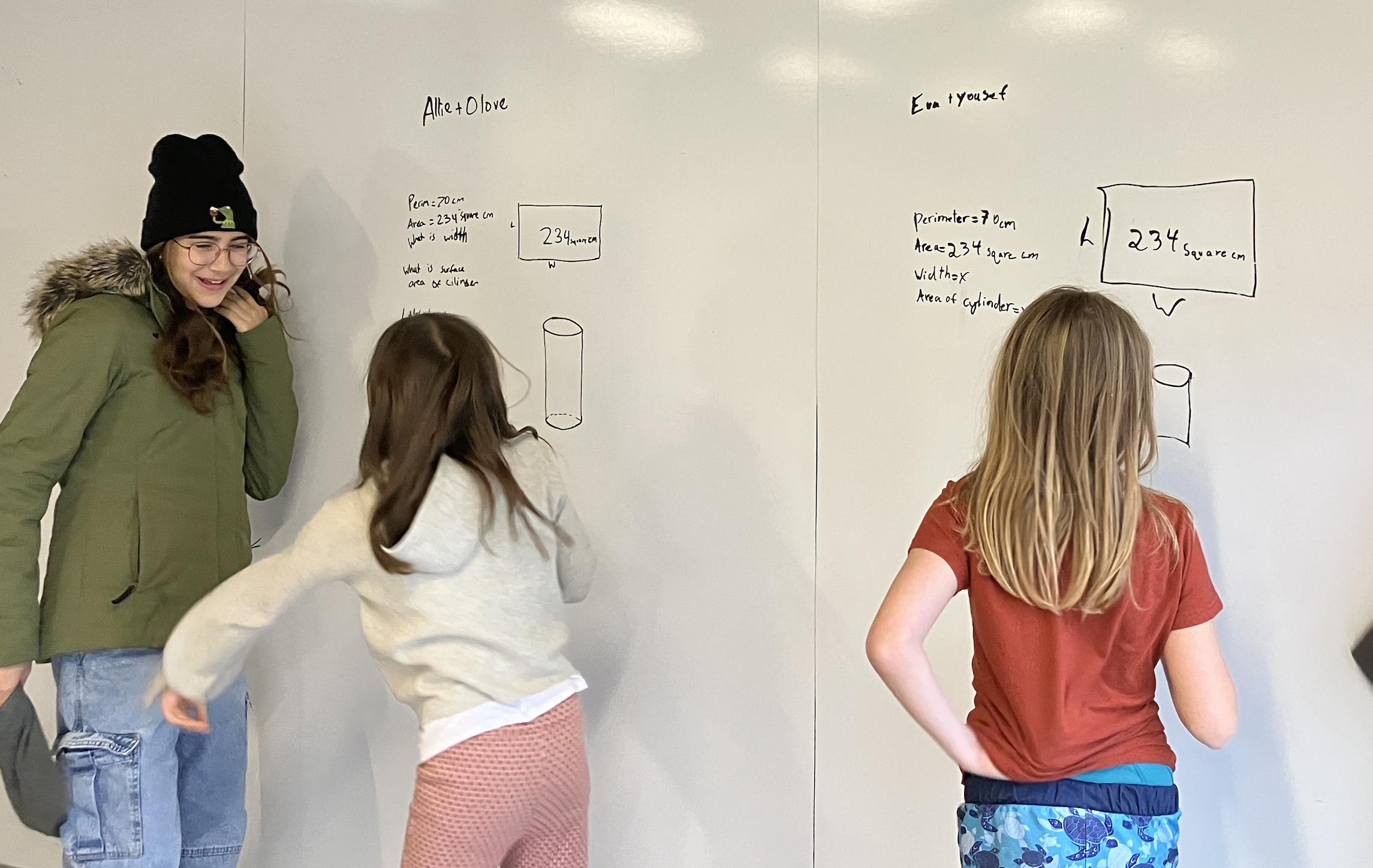Intellectual Fearlessness in Math
Early in the year, Mr. Mann brought a challenging concept to Math Block in Sage and Crimson Bands. It wasn’t exclusively a math concept, but an invitation to think differently about risk-taking. What does it mean to be intellectually fearless?
The phrase "intellectual fearlessness” comes from the book Thinking, Fast and Slow, by psychologist and economist Daniel Kahneman. When Mr. Mann introduced the concept, learners recognized fearlessness as a sort of bravery that, to the observer, presents as a lack of fear. They observed that while a person might have the experience of feeling afraid but taking action anyway, that same person might seem “fearless” to others.
Sage and Crimson learners also grappled with the term “intellectual,” which they defined as “of or relating to the mind.” They connected the attribute with learning and conjectured that “the growth of the mind is learning.” One learner posited that intellectual fearlessness was simply “the willingness to learn.”
Ideas kept building as another young learner suggested that being intellectually fearless would include being vulnerable. One of her peers added that being fearless would then mean you were not afraid to be thought of as not intellectual. That is, he suggested that you’d be willing to take risks to share your ideas even when you might be unsure or mistaken. This discussion laid the groundwork for experiences that lay ahead.
Sharing the concept of intellectual fearlessness with kids is only part of the work. How do we create the conditions for them to put it into practice? At Long-View, one of our core assumptions is that learners have a significant capacity for understanding. When we make space for failure, learners test that capacity, stretching it in the process. So, what kinds of mathematical experiences invite kids to take intellectual risks, to try out steps in thinking that they’re not sure of? How do we plan if we want them to engage in that way?
With these questions in mind, Mr. Mann created a set of especially “gnarly” thought exercises and set out to observe learners’ behaviors related to intellectual fearlessness in that context. Two threads emerged. Some learners tended to assess the situation, decide “This is too hard,” and shut down. Others approached the difficulty with an attitude of “What could I do with it? What could we try?”
Mr. Mann explained how, when one partnership from Crimson Band, Harrison and Reese, “dug in and tried to do something, they mathematically tied themselves in a knot – but they were trying something, they were attempting something – they had let things get messy.” When we encourage this kind of work in math, it goes against the grain of “the standard approach to math where you should quickly and efficiently get to the correct answer, rather than letting things get messy, trying things, and then iterating.”
Mr. Mann brought another of these gnarly thought exercises to Sage Band on a Monday morning in late January. In planning the exercise, Mr. Mann predicted, “I have a prompt that’s probably going to break everybody: I’m going to tell them so little about a rectangle and then I’ll ask them, ‘What would the surface area of the cylinder be if you rotated that rectangle in space through an axis of symmetry?’ Half the room is gonna be like, I cannot even imagine that….”
When learners engage in the set of thought exercises known at Long-View as “Translating Expressions and Equations,” they must take in the information from the prompt just by listening – they don’t receive a written version. Learners hear the prompt three times. They know the routine: the first time, you just listen, then head for a whiteboard with your math partner. The second time, you take notes. The third time (which occurs after some delay), you check your understanding after working with the information for a little while at whiteboards.
As Sage Band sat in the conversation lounge on that Monday morning, Mr. Mann read the prompt aloud:
The perimeter of a rectangle is 70 cm. The area of the rectangle is 234 cm². What is the width of the rectangle?
A cylinder is formed by rotating the rectangle around the longer of its two axes of symmetry. What is the surface area of the cylinder?
Learners got up from the red sofas and headed for partnerships, already chewing on the prompt. Many began by drawing rectangles and cylinders on their whiteboards. When Mr. Mann read the prompt again, they added in the numbers.
While most groups stood at their whiteboards, expo markers in hand, a blur of motion appeared at the center of the room. Hieu looked on as Lucas knelt on the floor, holding a clipboard upright. He spun it around, demonstrating how rotating the board would create a cylinder if you followed its motion through time.
A few minutes later, Lucas and Hieu presented their thinking in a what we call a “Public Share.” Mr. Mann’s notes record that the band “talked about how we might think about the surface area of the cylinder. Lucas helped many of the learners see that there would be two circular bases. There was uncertainty about how to consider the lateral surface area. Juliet and William led them to see it would be a rectangle, but the dimensions were not clear.”
As he reflected on the thought exercise a few days later, Mr. Mann explained more about the way he designs experiences to elicit intellectual risk-taking. This particular exercise “might have been too challenging for some learners, but had components that were accessible to all of them. This level of difficulty gives them a reason to find their way into grappling with something challenging.”
He continued: “I want them to develop spatial reasoning in part because it’s useful, and in part because it’s an intellectual challenge.” Faced with that challenge, “some get overwhelmed and check out,” which gives a teacher an opportunity to coach toward a starting place and towards a mindset shift.
This kind of exercise also allows a teacher to find areas of understanding that need work. In this case, Mr. Mann could see a need to do more work on reasoning with systems of equations. Some previous knowledge of concepts like finding circumference seemed to have fallen apart, as the band hadn’t revisited them in a while, which led Mr. Mann to design a sidebar on circumference for a subsequent block. Nonetheless, what really struck Mr. Mann about this thought exercise was to see how far learners got anyway, despite gaps in background knowledge.
“If I give learners problems that are too simple,” Mr. Mann explained, “I don’t learn the limits of their knowledge, and there’s no reason for them to collaborate.” Conversely, when something is really difficult, we have to reach out to others and work together to understand it. “I want them to have that experience,” he said.